データ分析に役立つ！ 正規分布をマスターしよう

１　3分の2の顧客の目線に合う価格帯と、品ぞろえの割合は？

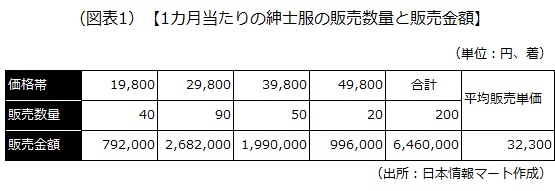
突然ですが、質問です。あなたは紳士服店を運営しており、図表1の過去の売り上げデータに基づいて、紳士服の価格帯ごとの品ぞろえを見直そうと思っています。紳士服の購入を考えている顧客のうち、3分の2の人の目線に合う価格帯で品ぞろえをするには、どうすればよいでしょうか？　また、それぞれの価格帯ごとの紳士服の品ぞろえの割合は、どのように配分すればよいでしょうか？

この答えを推測するときに活用できるのが正規分布です。正規分布は統計学における確率分布の一つで、

平均値に該当するものの数が最も多く、平均から外れる度合いに応じて、一定の割合で該当するものの数が減っていく

ことを前提としたモデルです。このため、正規分布をグラフにすると、中心が高く盛り上がって、両端に行くほど緩やかに低くなっていく、左右対称で釣り鐘のような形になります。

この記事では、データ分析の際に正規分布を活用できるようになるために、正規分布の前提となる「分散」と「標準偏差」の考え方を含めて解説します。なお、冒頭の質問の答えは、この記事を読んでいくうちに分かるようになっています。正規分布は統計学では基本的な分野であり、考え方を押さえておくと、日ごろのビジネスシーンでも活用できます。ぜひ参考にしてみてください。

２　平均と最頻値

「平均」はデータを全て足した合計値を、そのデータ数で割った値になります。また、最頻値とは、そのデータの中で最も頻繁に出現する値になります。

図表1の紳士服の平均販売単価は、次の式で算出することができます。

19,800（円）×40（着）＋29,800（円）×90（着）＋39,800×50（着）＋
49,800（円）×20（着）／200（着）=32,300（円）

販売数量は合計200着、販売金額は合計646万円です。紳士服1着当たりの平均販売単価は3万2300円となります。また、4つの価格帯で最もよく売れているのは2万9800円の90着です。この場合、販売数量の最も多い2万9800円が最頻値となります。

しかしながら、3分の2の顧客の目線に合う価格帯で販売するには、この４つの価格帯でよいのでしょうか？　それを推測するのに役立つのが、「分散」と「標準偏差」です。

３　分散と標準偏差

データのばらつきを表す尺度として、分散と標準偏差があります。聞き慣れない言葉かもしれませんが、試験でおなじみの「偏差値」で説明すると身近に感じられるでしょう。

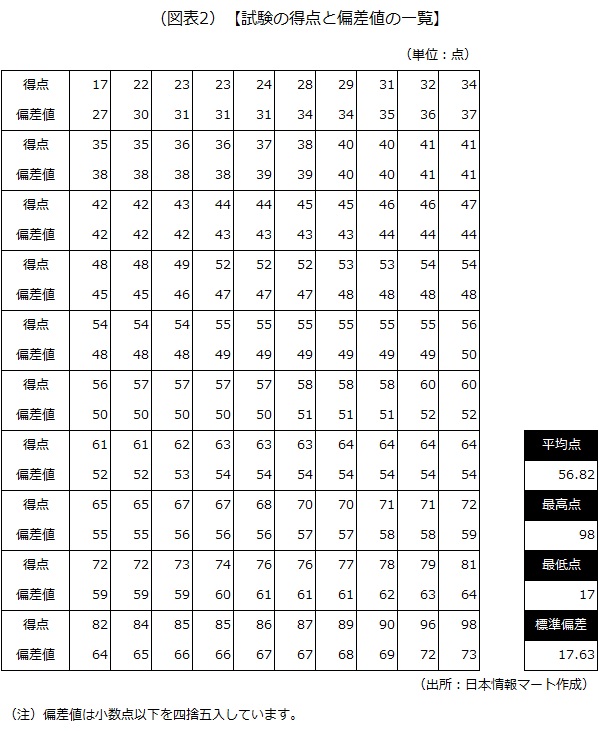
例えば、100人が受けたある試験の得点と偏差値の一覧を表すと次の通りになります。

偏差値は「高い、低い」といった具合に使われます。偏差値はその試験を受けた人の中で、自分がどのくらいの位置にいるかを知るのに便利です。ここでは偏差値を利用してデータのばらつきについて、また、データのばらつきを表す標準偏差について説明します。

偏差値は受験者の中での位置を示します。偏差値50が受験者全体の中心で、平均点が偏差値50になります。平均点に対して得点が高いか低いかで、偏差値が50超か以下かに分かれます。

偏差値は次の式で算出することができます。

偏差値＝（得点－平均点）／標準偏差×10＋50

標準偏差は統計値のばらつきを表す数値で、標準偏差を2乗したものを分散といい、同様に統計値のばらつきを表します。分散と標準偏差は次の式で算出することができます。

例えば、最高点98点と平均点（56.82点）の差は41.18点（98点－56.82点）です。この41.18点を標準偏差（17.63）で割ると2.34となります。2.34に10を乗じて50を加えると偏差値73.4を算出することができます。

偏差値は、得点が平均点からどれだけ離れているかの標準偏差を尺度として測り、分かりやすくするために平均を50、1標準偏差を10として算出しています。

98点は平均点から標準偏差2.34個分離れていることを表しています。つまり、偏差値73.4（23.4+50）と表示しています。偏差値10ポイントは標準偏差1個分に相当します。逆算すれば、偏差値73.4は平均である50から23.4個分離れたところに位置しており、これは10の2.34個分（23.4／10）に相当します。

図表2【試験の得点と偏差値の一覧】の試験の得点の分布は次の通りです。

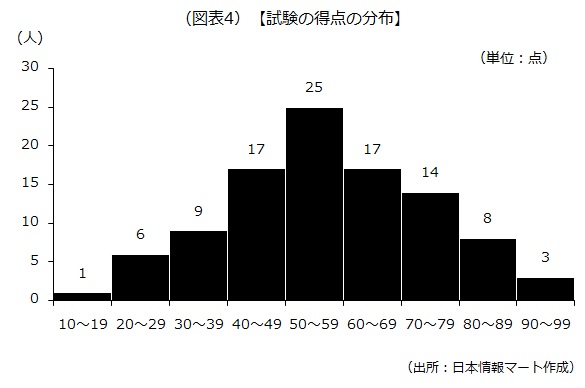
得点の分布は50～59点が最も多く、得点が高く、または得点が低くなるほど、数は減っています。なお、試験の内容が簡単すぎる場合には平均点は上がり、逆に難しすぎる場合には平均点は下がります。また、得点の分布によって標準偏差は大きくもなれば小さくもなります。

標準偏差はデータのばらつきを表し、標準偏差が大きいほどデータのばらつきが大きく、標準偏差が小さいほどデータのばらつきが小さいことを示します。

４　正規分布を使って、3分の2の顧客の目線に合う紳士服の価格帯を算出する

さて、分散と標準偏差について説明しましたので、この記事の冒頭で質問した「3分の2の顧客の目線に合う紳士服の価格帯」を算出してみましょう。

正規分布の標準偏差で覚えておくべきルールとして、

平均値から標準偏差±1の範囲内に含まれるデータは全体の68.26％を占める
平均値から標準偏差±2の範囲内に含まれるデータは全体の95.44％を占める

ことを押さえておきましょう。これは正規分布表を説明する際に詳述します。

まず、図表1【1カ月当たりの紳士服の販売数量と販売金額】のデータを基に、販売価格の分散と標準偏差を算出します。

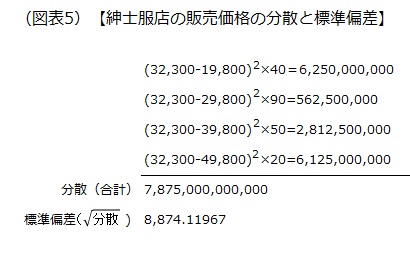
標準偏差は8874円となりました。標準偏差の上下1の価格帯で3分の2の顧客が収まりますから、平均販売価格である3万2300円の上下8874円、つまり2万3426円から4万1174円の価格帯であれば、およそ3分の2の顧客の目線に合うことが推測できます。

従って、3分の2の顧客を意識するのであれば、1万9800円、3万9800円の紳士服は品ぞろえする必要がないということになります。代わりに2万3426円と4万1174円の紳士服を品ぞろえすることにします。

では、新たな4つの価格帯の紳士服は、何着ずつ品ぞろえすればよいのでしょうか？　そのためには、正規分布表について理解する必要があります。

５　正規分布表

1）正規分布の基本

社会現象や自然現象の中に表れるばらつきの多くは釣り鐘形をした正規分布になる傾向があります。身近なものでは身体測定や健康診断のデータ（身長・体重・血圧・脈拍数など）は正規分布になります。

以降では、男性の身長を事例に挙げて解説していきます。17歳男性の平均身長が170.7センチメートル、標準偏差が5.73センチメートルであると仮定します。これを基に身長の分布図を示すと次の通りです。

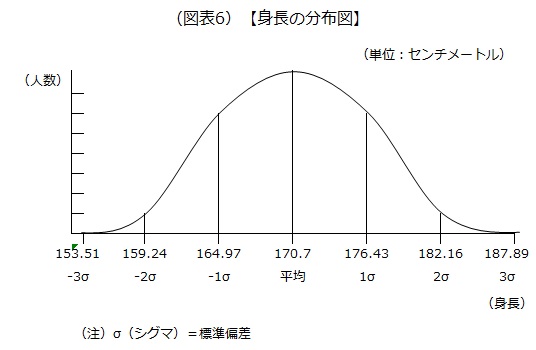
図表6では標準偏差を便宜上σ（シグマ）という記号で表しています。1σ＝5.73センチメートルです。

正規分布では、平均から1σの範囲にデータの34.13％が分布し、同様に平均から2σの範囲に47.72％、平均から3σの範囲に49.87％が分布するとされています。詳しくは後述する正規分布表で確認することができます。

従って、170.7～176.43センチメートルの間には全体の34.13％が分布し、170.7～182.16センチメートルには47.72％が分布することになります。同様に164.97～170.7センチメートルには34.13％が分布し、159.24～170.7センチメートルには47.72％が分布することになります。

例えば、17歳男性が1000人いるとした場合、身長が182.16センチメートルを超える男性は25人（1000人×｛100％－（50％＋47.42％）｝＝25.8人）いると推測できます。

図表6の身長の分布図の平均を0とした場合の身長の分布図を示すと次の通りです。

2）正規分布表の見方

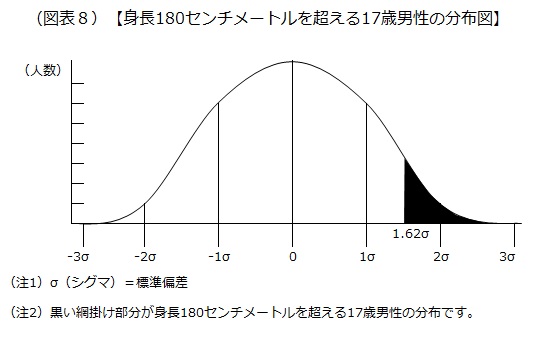
例えば、身長が180センチメートルを超える17歳男性の割合はどの程度かを調べる場合、次のようにします。

（180センチメートル－平均身長）／標準偏差
＝（180－170.7）／5.73＝1.62

1.62σを超える男性の割合、図表8の黒い網掛け部分の割合が分かればよいのです。

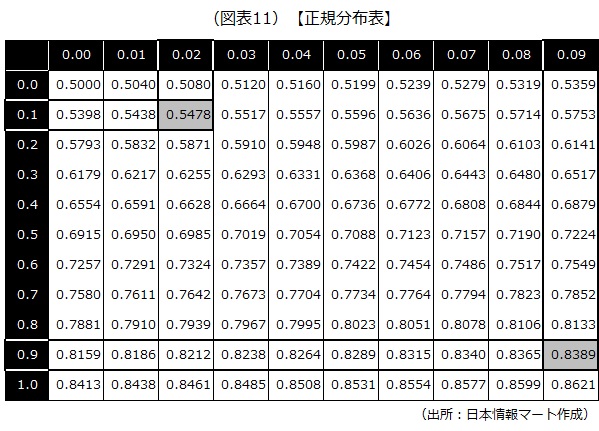
図表9は正規分布表です。表の利用方法について説明します。

まず、1.62σを1.6と0.02に分けます。表左側の網掛け部分の列0.0～2.0の中から1.6を探します。次に表上段の網掛け部分の行0.00～0.09の中から0.02を探します。そして、1.6と0.02が交差する部分が0.9474（網掛け部分）となっています。

これは、身長が180センチメートル以下の男性は、全体の94.74％を占めることを示しています。従って、身長が180センチメートルを超える男性の割合は5.26％（100％－94.74％）ということが分かります。

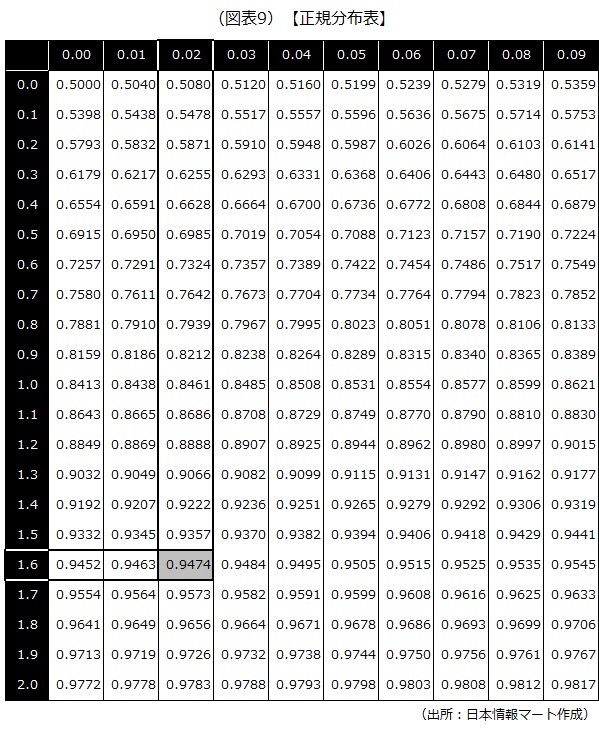
図表9は平均を0としています。0.0と0.00の交差する部分は0.5000であり、平均値以下には50％が分布していることを意味しています。

3）正規分布表の応用

続いて、正規分布表の応用として、身長165～170センチメートルの男性の割合を推測してみましょう。

平均身長と標準偏差を使って、身長165センチメートルは平均身長（170.7センチメートル）から標準偏差（5.73センチメートル）の何個分離れているか、また、170センチメートルは平均身長（170.7センチメートル）から標準偏差（5.73センチメートル）の何個分離れているかを調べます。

平均身長から身長165センチメートルまでの標準偏差の数
＝（165－170.7）／5.73＝－0.99
平均身長から身長170センチメートルまでの標準偏差の数
＝（170－170.7）／5.73＝－0.12

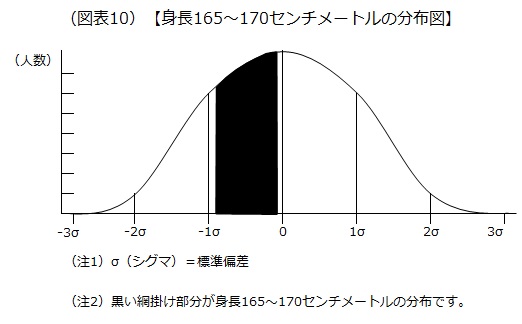
正規分布は平均を中心として左右対称なので、身長165～170センチメートルの男性の占める割合は、下表（正規分布表）の0.1と0.02の交差する0.5478、0.9と0.09の交差する0.8389を基に、次の通り推測することができます。

0.8389－0.5478＝0.2911→29.11％

６　正規分布表を使って、新たな価格帯の紳士服を何着ずつ品ぞろえすればよいかを算出する

それでは最後に、正規分布表を使って算出した新たな価格帯（2万3426円、2万9800円、3万9800円、4万1174円）の紳士服を、合計200着で換算すると何着ずつ品ぞろえすればよいのかを図表で示します。

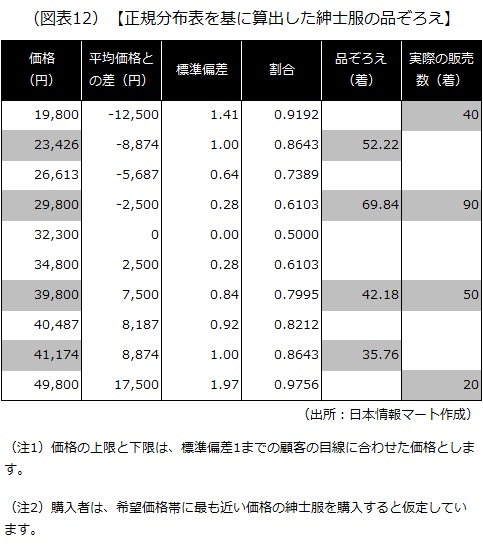
つまり、3分の2（標準偏差1）の顧客の目線に合わせて2万3426円、2万9800円、3万9800円、4万1174円の4つの価格帯の紳士服を販売する場合、正規分布表を基にした適正な品ぞろえは、合計200着で換算すると、それぞれ52着、70着、42着、36着ということになります。

以上（2021年10月）

pj70055
画像：Andrey Popov-Adobe Stock