1 PERTを使えばプロジェクトの滞留を予防できます!
2 PERT図の作成方法
3 PERTを機能させる3つのポイント
4 とにかく「クリティカルパス」をケアする
5 小規模なプロジェクトでは逆に非効率
1 PERTを使えばプロジェクトの滞留を予防できます!
突然ですが、皆さんの会社のプロジェクトで次のような状態になった経験はありませんか?
- 多くの工程は順調なのに、特定の工程がネックになって滞ってしまった
- 作業を均等に分担したはずなのに、ある担当者だけはいつも暇そうだ
- プロジェクトが進んでいないが、どこで止まっているのか分からない
こうした経験のある方にご紹介したいのが、
PERT(Program Evaluation and Review Technique)
です。PERTとは、
1つ1つの作業工程を「前の工程が終わらないと次の工程が始められない」という依存関係に従って矢印でつないでいき、それぞれの工程に所要時間を記入していく手法
です。PERTを進めるための「PERT図」を作成することで、
- 各工程にどのくらいの時間が必要なのか
- 各工程がどのような関係にあるのか
- どのような順序で進めればよいのか
といったことが「見える化」できます。この記事では、PERT図の作成方法と具体的な使い方を解説します。
2 PERT図の作成方法
1)必要な作業を洗い出し、所要時間を算出する
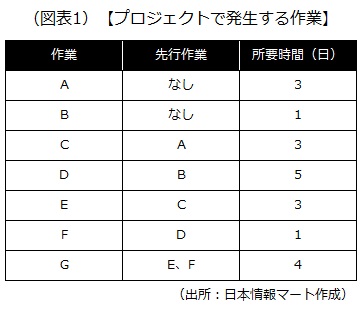
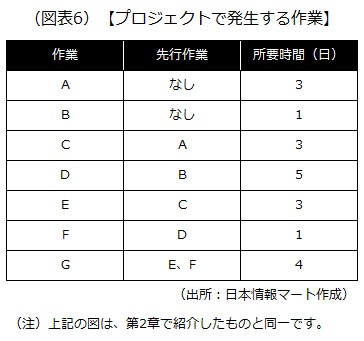
例えば、あるプロジェクトで必要な作業がA~Gに分けられるとします。各作業の前後関係を明らかにし、それぞれの所要時間を「日」単位で算出してみると、次のようにまとめられます。
まず、次の3種類の時間を見積もります。
- 楽観的推定時間(a):作業が何の問題もなく順調に進んだ場合の時間
- 推定所要時間(b):同様の作業の実績などから妥当だと見積もられる時間
- 悲観的推定時間(c):問題が発生したため想定以上にかかる時間
推定所要時間で作業が完了する確率が最も高いという前提で、それぞれに重み付けをして平均値を算出します。重みは、推定所要時間が4、楽観的推定時間と悲観的推定時間はそれぞれ1とし、以下の式で所要時間を算出します。
- 所要時間=(a+4×b+c)/6
2)各作業の関係を矢印で結ぶ
PERTでは各作業の関係を「○」と「→」で示します。これをアローダイヤグラムといいます。
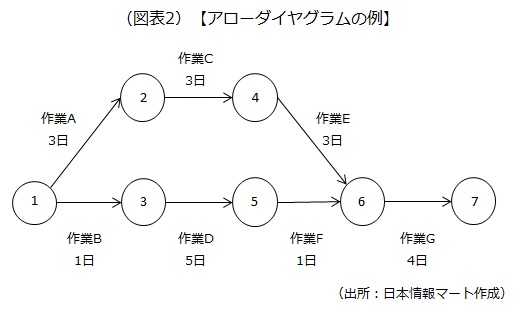
「○」は「ノード」と呼ばれ、各作業の始まりと終わりを表します。「→」は、それぞれの「作業」を表します。PERTでは「作業」のことを「アクティビティ」といいますが、この記事では説明を分かりやすくするために「作業」と表記します。また、「作業A」などの作業名の下には、各作業にかかる所要時間(ここでは「日」単位)を記載します。なお、ノードに振られた番号は以降の説明のために付与したもので、それ自体に意味はありません。
アローダイヤグラムは、プロジェクトの全体像と各作業間の関係を表しています。例えば、「作業C」を始めるためには、その前工程である「作業A」を終了させなければなりません。また、「作業A→C→E」と「作業B→D→F」は、独立した一連の作業なので並行して進められますが、両方が終わらないと「作業G」は始められません。
3 PERTを機能させる3つのポイント
1)最早結合点時刻:全作業の所要時間を把握する
最早結合点時刻とは、当該ノードの次の作業を開始するために最低限必要となる時間です。例えば、ノード4の最早結合点時刻は6日です(作業Aの3日と作業Cの3日の合計)。また、ノード6の最早結合点時刻は9日です。ノード6にたどり着くには、「作業A→C→E」の9日と、「作業B→D→F」の7日が必要ですが、時間の多くかかる9日が最早結合点時刻となります。この考え方に基づき、最早結合点時刻を網かけで示すと次のようになります。
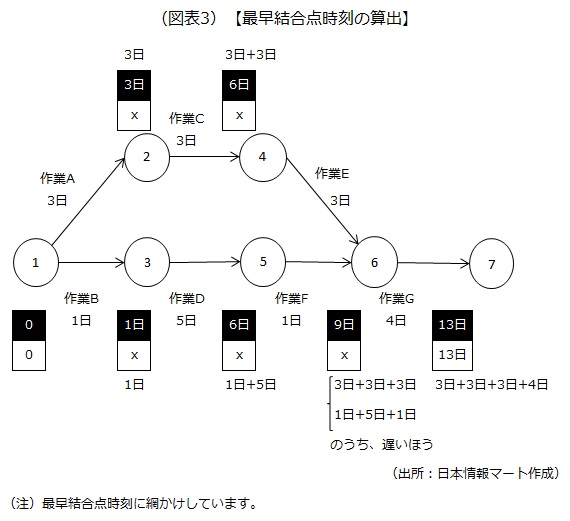
なお、下段には最遅結合点時刻が入ります。まだ算出していないので、便宜上「x」としていますが、始点(ノード1)と終点(ノード7)は、最早結合点時刻と同じになります。
2)最遅結合点時刻:各作業のデッドラインを把握する
最遅結合点時刻とは、以降の作業が遅れないようにするために当該ノードに到達しなければならない最も遅い時刻です。いわゆる「デッドライン」です。最遅結合点時刻は、次のノードの最遅結合点時刻から、それらのノードをつなぐ作業の所要時間を差し引いて算出します。
ノード6の場合、次のノード7の最遅結合点時刻は13日なので、作業Gの所要時間4日を差し引いた9日(13日-4日)が最遅結合点時刻です。この考え方に基づき、最遅結合点時刻を網かけで示すと次のようになります。
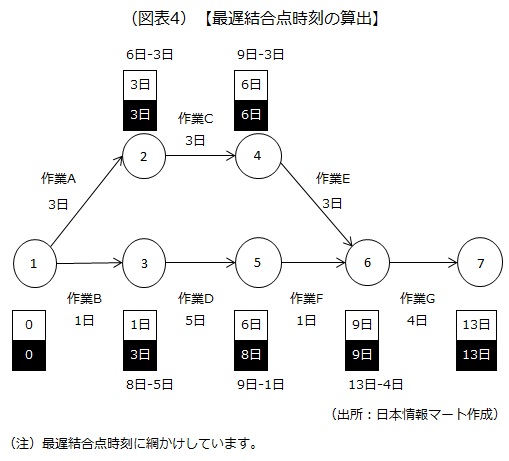
なお、通常は、始点と終点の最遅結合点時刻は最早結合点時刻と同じにしますが、プロジェクトの締め切りを終点の最遅結合点時刻として設定し、そこから各ノードの最遅結合点時刻を算出していくこともできます。
3)クリティカルパス:要注意の作業を把握する
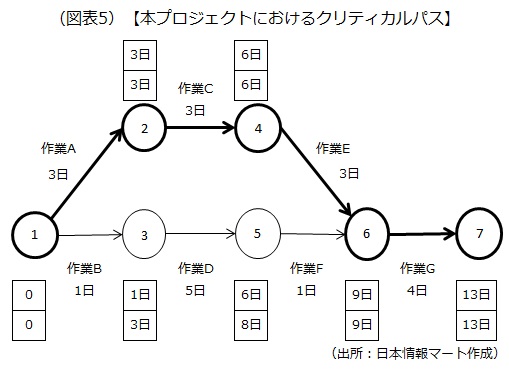
図表4の「最遅結合点時刻の算出」を見ると、「作業A→C→E→G」の最早結合点時刻と最遅結合点時刻が同じです。つまり、スケジュールに余裕がないということです。このように、プロジェクト全体のスケジュールに影響を及ぼす経路を「クリティカルパス」といい、スケジュール管理に当たって最も注意しなければなりません。クリティカルパスは、太い矢印で分かりやすく示します。
なお、「作業B→D→F→G」については、最早結合点時刻と最遅結合点時刻に2日の差があります。これは、2日の余裕があることを意味します。つまり、クリティカルパスではありません。
4 とにかく「クリティカルパス」をケアする
ここでは前章までに例として挙げたプロジェクトを題材に、PERTを利用して、プロジェクト全体の効率化を図るための考え方を紹介します。プロジェクトで発生する作業および作業のアローダイヤグラムは次の通りです。
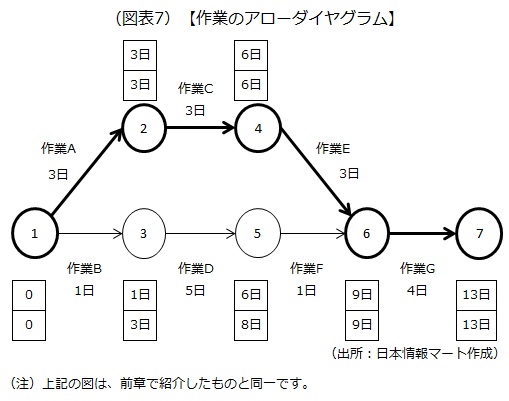
作業Dの所要時間が5日と最も長いので、ここに資源を集中して短縮しようと考えるかもしれません。しかし、「作業B→D→F」が早く完了しても、クリティカルパスである「作業A→C→E」が完了しなければ作業Gには進めません。むしろ、作業Dを短縮したことで待ち時間が延びます。そうではなく、クリティカルパス上の作業の短縮が必要です。
その際、クリティカルパスの変化に注意しましょう。資源を集中し、「作業A→C」を計3日で完了できるようにした場合、作業Eの3日を加えても「作業A→C→E」の所要時間は6日となり、「作業B→D→F」の所要時間である7日を下回ります。この時点で、クリティカルパスは「作業B→D→F→G」に変わりました。しかし、これに気付かずに、作業Eにさらに資源を投入して所要時間の短縮を図っても、プロジェクト全体の効率化にはつながりません。
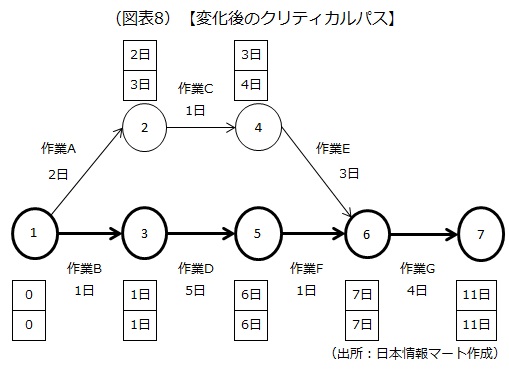
5 小規模なプロジェクトでは逆に非効率
PERTではアローダイヤグラムを作成しますが、そのためには作業の細分化、作業順序の特定、所要時間の見積もりなどの準備が必要です。これらの準備は大変ですが、手を抜くと「想定とクリティカルパスが違う」などの問題が生じます。作業数が少ない小規模なプロジェクトならアローダイヤグラムは簡単に作成できますが、そもそもPERTを利用するまでもなく進められるので、無理にPERTを利用するのは非効率です。
以上(2025年1月更新)
pj40024
画像:ribkhan-Adobe Stock