文系の経営者にも分かりやすい定量的な経営判断

１　難しい意思決定を求められる経営者

経営の意思決定は、

確信を持てることなどほとんどなく、不確実性やトレードオフ（一方を追求すれば、他方を犠牲にせざるを得ない二律背反の状態）の中で行われる

ものです。会社の命運を分ける重要な決定もあるので、経営者は意思決定のよりどころを求めます。物事を考える際は、

の両面から捉えますが、定性的な部分は経営者個人のものです。ですので、この記事では、定性的な考え方を補完するものとして、定量的な6つの考え方を示します。統計の知識がなくても理解できるように簡易に示していますので、参考にしてください。

２　確率を考慮した意思決定手法

1）意思決定に当たっての前提条件

ここから、皆さんは衣料品店の社長になっていただきます。今、冬物衣料を販売するに当たり、メーカーに発注する量を検討しているのですが、季節商品なので追加発注はできません。厳冬ならば平年を上回る売上高が見込めますが、暖冬ならば売上高は減少します。過去のデータを基に推計した結果、冬の気象と売上高予測の関係は次の通りです。

平年並みなら売上高は1億円を見込めます。また、厳冬なら売上高は平年の10％増の1億1000万円、しかし、暖冬なら売上高は平年の10％減の9000万円しか見込めません。

2）仕入高と気象と営業利益の関係

長期気象予報によると、今季の冬は厳冬となる確率が20％、平年並みとなる確率が50％、暖冬となる確率が30％です。冬物衣料の仕入計画としては、次の3つの案があります。

もし、厳冬と予想したのに暖冬になった場合、売れ残り商品が大量に発生し、値引き販売などによって処分しなければなりません。逆に、暖冬と予想したのに厳冬になった場合、在庫が底を突いて販売する商品がなくなってしまいます。気象ごとの仕入高と営業利益金額の関係は次の通りです。

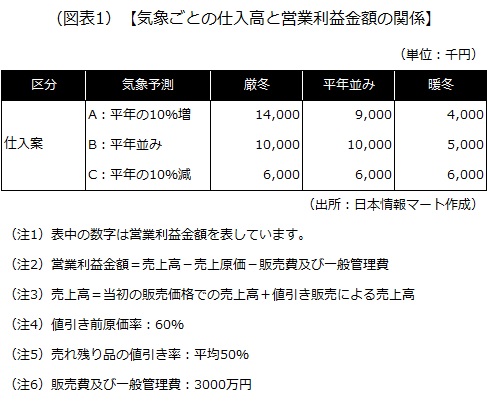
厳冬と予想して仕入高を平年の10％増とし、実際に厳冬であれば1400万円（1億1000万円－1億1000万円×60％－3000万円）の営業利益が見込めます。しかし、予想が外れて暖冬になった場合、400万円（9000万円＋（1億1000万円－9000万円）×50％－1億1000万円×60％－3000万円）となります。

3）期待値原理

期待値は、予想される利益に発生する確率を乗じた総和をいいます。

期待値＝∑（気象ごとの営業利益金額×気象の発生確率）

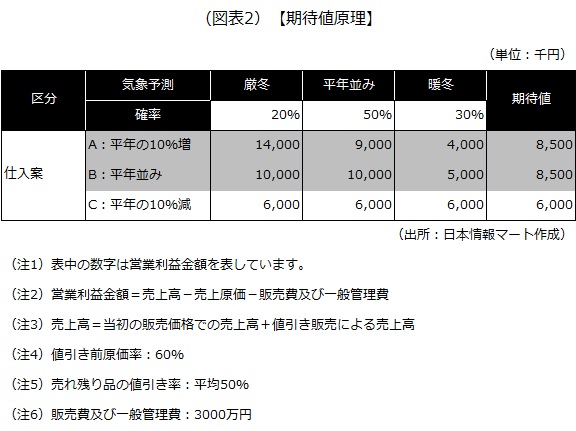
図表2の仕入案A・B・Cの期待値は次の通りです。

期待値が最も大きいのはA案およびB案の850万円です。期待値原理によると、A案かB案のいずれかを選択することになります（図表2の網掛け部分）。

4）最尤（さいゆう）未来原理

最尤未来原理による意思決定は、明快な方法で、起きる可能性の最も高い中から利益の一番大きいものを選ぶ手法です。

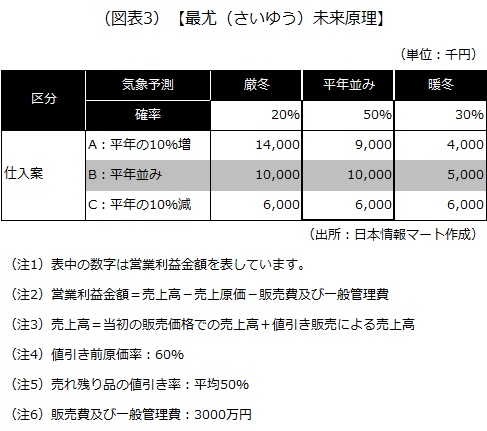
最尤未来原理によると、発生する確率の最も高い平年並みのB案を選択することになります。

３　確率が不明な場合の意思決定手法

1）等可能性の原理

期待値原理と最尤未来原理は発生の確率を考慮したものですが、発生の確率が分からない場合もあります。ここからは、確率が分からない場合の意思決定手法について、引き続き、冬物衣料の仕入案のケースを用いて説明します。

等可能性の原理による意思決定は、厳冬の確率、平年並みの確率、暖冬の確率がどれも1／3で同じと考えて意思決定する手法です。

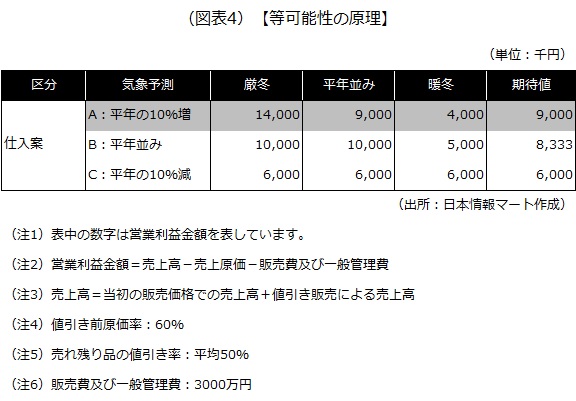
期待値の算出方法は次の通りです。

等可能性の原理によると、期待値が最も高いA案を選択することになります。

2）悲観的態度を反映した決定原理

悲観的態度を反映した決定原理による意思決定は、最悪の事態において、最大の利益が確保できることを念頭に置いた手法です。最も売上高が小さくなる暖冬のときに、最も大きな利益が確保できる仕入案を選択することになります。

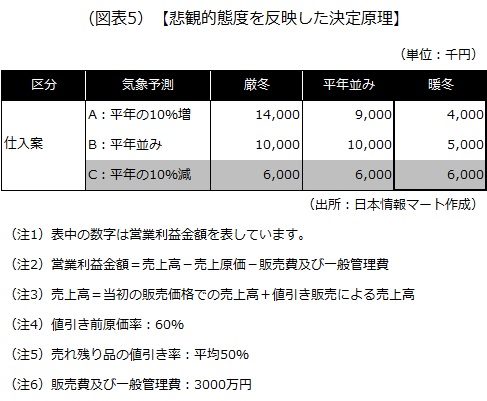
悲観的態度を反映した決定原理によると、先の冬物衣料の仕入案のケースでいえば、暖冬のケースを想定して、その中で最も営業利益金額が大きいC案を選択することになります。

3）楽観的態度を反映した決定原理

楽観的態度を反映した決定原理による意思決定は、最大の利益が確保できることを念頭に置いた意思決定手法です。最も売上高が大きくなる厳冬のときに、最も大きな利益が確保できる仕入案を選択することになります。

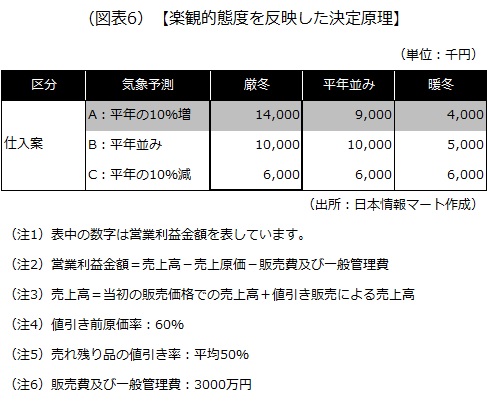
楽観的態度を反映した決定原理によると、先の冬物衣料の仕入案のケースでいえば、厳冬のケースを想定して、その中で最も営業利益金額が大きいA案を選択することになります。

4）楽観的態度と悲観的態度を含めた決定原理による意思決定

楽観的態度と悲観的態度を含めた決定原理による意思決定は、楽観的態度を反映した決定原理による意思決定と、悲観的態度を反映した決定原理による意思決定の中間に位置付けられる手法です。

ここでは楽観的態度について楽観度係数を用いて表現します。先の仕入案で説明すると次のようになります。

決定係数＝見込める最大の利益×楽観度係数＋見込める最小の利益×（1－楽観度係数）

楽観度係数は0以上1以下に設定されます。楽観度係数が最低の0のとき、決定係数は悲観的態度を反映した決定原理と同じになります。また、楽観度係数が1で最大のとき、決定係数は楽観的態度を反映した決定原理と同じになります。

仮に、楽観度係数を0.7として、仕入案Aの決定係数を算出すると次の通りです。

仕入案Aの決定係数＝1400万円×0.7＋400万円×（1－0.7）＝1100万円

楽観的態度と悲観的態度を含めた決定原理に基づく楽観度係数別の営業利益金額は次の通りです。

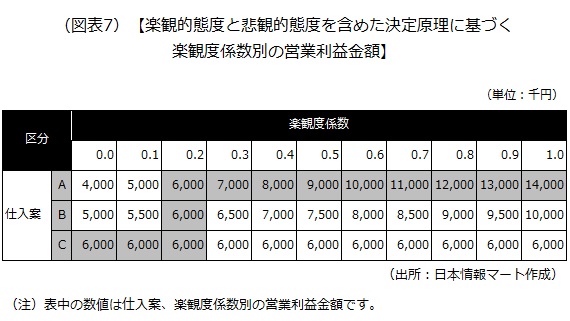
楽観的態度と悲観的態度を含めた決定原理による場合、楽観度係数によって結果が大きく変わります。楽観度係数の中間である0.5を平均とすると、0.5未満は消極的、0.5以上は積極的といえます。消極的でリスクを取らない経営者は楽観度係数0.5未満を、積極的でリスクを取る経営者は楽観度係数0.5以上を見積もることになるでしょう。

以上（2022年11月）

pj10052
画像：pixabay